Kirchhoff's current law (KCL)

This law is also called Kirchhoff's point rule, Kirchhoff's junction rule (or nodal rule), and Kirchhoff's first rule.

The principle of conservation of electric charge implies that:

At any node (junction) in an electrical circuit, the sum of currents flowing into that node is equal to the sum of currents flowing out of that node.
Adopting the convention that every current flowing towards the node is positive and that every current flowing away is negative (or the other way around), this principle can be stated as:


n is the total number of branches with currents flowing towards or away from the node.

This formula is also valid for complex currents:


The law is based on the conservation of charge whereby the charge (measured in coulombs) is the product of the current (in amps) and the time (which is measured in seconds).

Changing charge density
Physically speaking, the restriction regarding the "capacitor plate" means that Kirchhoff's current law is only valid if the charge density remains constant in the point that it is applied to. This is normally not a problem because of the strength of electrostatic forces: the charge buildup would cause repulsive forces to disperse the charges.

However, a charge build-up can occur in a capacitor, where the charge is typically spread over wide parallel plates, with a physical break in the circuit that prevents the positive and negative charge accumulations over the two plates from coming together and cancelling. In this case, the sum of the currents flowing into one plate of the capacitor is not zero, but rather is equal to the rate of charge accumulation. However, if the displacement current dD/dt is included, Kirchhoff's current law once again holds. (This is really only required if one wants to apply the current law to a point on a capacitor plate. In circuit analyses, however, the capacitor as a whole is typically treated as a unit, in which case the ordinary current law holds since exactly the current that enters the capacitor on the one side leaves it on the other side.)

More technically, Kirchhoff's current law can be found by taking the divergence of Ampère's law with Maxwell's correction and combining with Gauss's law, yielding:


This is simply the charge conservation equation (in integral form, it says that the current flowing out of a closed surface is equal to the rate of loss of charge within the enclosed volume (Divergence theorem)). Kirchhoff's current law is equivalent to the statement that the divergence of the current is zero, true for time-invariant ρ, or always true if the displacement current is included with J.

Kirchhoff's circuit laws

Kirchhoff's circuit laws are two equalities that deal with the conservation of charge and energy in electrical circuits, and were first described in 1845 by Gustav Kirchhoff. Widely used in electrical engineering, they are also called Kirchhoff's rules or simply Kirchhoff's laws (see also Kirchhoff's laws for other meanings of that term).

Both circuit rules can be directly derived from Maxwell's equations, but Kirchhoff preceded Maxwell and instead generalized work by Georg Ohm.



Kirchhoff's voltage law (KVL) The sum of all the voltages around the loop is equal to zero. v1 + v2 + v3 + v4 = 0This law is also called Kirchhoff's second law, Kirchhoff's loop (or mesh) rule, and Kirchhoff's second rule.

The directed sum of the electrical potential differences around any closed circuit must be zero.
Similarly to KCL, it can be stated as:


Here, n is the total number of voltages measured. The voltages may also be complex:


This law is based on the conservation of energy whereby voltage is defined as the energy per unit charge. The total amount of energy gained per unit charge must equal the amount of energy lost per unit charge. This seems to be true as the conservation of energy states that energy cannot be created or destroyed; it can only be transformed from one form to another.

Electric field and electric potential
Kirchhoff's voltage law as stated above is equivalent to the statement that a single-valued electric potential can be assigned to each point in the circuit (in the same way that any conservative vector field can be represented as the gradient of a scalar potential). Then the sum of the changes in this potential that occur as one makes an imaginary traverse around any closed loop in the circuit should be equal to zero.

This could be viewed as a consequence of the principle of conservation of energy. Otherwise, it would be possible to build a perpetual motion machine that passed a current in a circle around the circuit.

Considering that electric potential is defined as a line integral over an electric field, Kirchhoff's voltage law can be expressed equivalently as


which states that the line integral of the electric field around closed loop C is zero.

In order to return to the more special form, this integral can be "cut in pieces" in order to get the voltage at specific components.

This is a simplification of Faraday's law of induction for the special case where there is no fluctuating magnetic field linking the closed loop. Therefore, it practically suffices for explaining circuits containing only resistors and capacitors.

In the presence of a changing magnetic field the electric field is not conservative and it cannot therefore define a pure scalar potential—the line integral of the electric field around the circuit is not zero. This is because energy is being transferred from the magnetic field to the current (or vice versa). In order to "fix" Kirchhoff's voltage law for circuits containing inductors, an effective potential drop, or electromotive force (emf), is associated with each inductance of the circuit, exactly equal to the amount by which the line integral of the electric field is not zero by Faraday's law of induction.

Voltage divider

In electronics, a voltage divider (also known as a potential divider) is a simple linear circuit that produces an output voltage (Vout) that is a fraction of its input voltage (Vin). Voltage division refers to the partitioning of a voltage among the components of the divider.

The formula governing a voltage divider is similar to that for a current divider, but the ratio describing voltage division places the selected impedance in the numerator, unlike current division where it is the unselected components that enter the numerator.

A simple example of a voltage divider consists of two resistors in series or a potentiometer. It is commonly used to create a reference voltage, and may also be used as a signal attenuator at low frequencies.

MOSFETs

The most widely used and widely known FETs are MOSFETs (metal oxide semiconductor FETs), which come in NMOS (n-channel) and PMOS (p-channel) varieties. On a chip, NMOS and PMOS transistors are wired together in a complementary fashion to create CMOS logic, which is the most predominant and used in almost every electronic device today. See MOSFET and n-type silicon.

FETs and Bipolar

FET-based silcon chips are easier to construct than their bipolar counterparts. FETs switch a little slower than bipolar transistors, but use less power. Once the gate terminal on an FET has been charged, no more current is needed to keep that transistor on (closed) for the duration of time required. By comparison, a bipolar transistor requires a small amount of current flowing to keep the transistor on. While the current for one transistor may be negligible, it adds up when millions are switching simultaneously. The heat dissipated on bipolar limits the total number of transistors that can be built on the chip, which is why CMOS logic (based on FETs) is used to build chips with millions of transistors.

JFET

(Field Effect Transistor) One of two major categories of transistor; the other is bipolar. FETs use a gate element that, when charged, creates an electromagnetic field that changes the conductivity of a silicon channel and turns the transistor on or off. FETs are fabricated as individually packaged discrete components as well as by the hundreds of millions on a single chip.

Intensive and extensive properties

In the physical sciences, an intensive property (also called a bulk property), is a physical property of a system that does not depend on the system size or the amount of material in the system: it is scale invariant. By contrast, an extensive property of a system does depend on the system size or the amount of material in the system. (see: examples) Some intensive properties, such as viscosity, are empirical macroscopic quantities and are not relevant to extremely small systems.

For example, density is an intensive quantity (it does not depend on the quantity), while mass and volume are extensive quantities. Note that the ratio of two extensive quantities that scale in the same way is scale-invariant, and hence an intensive quantity.

Is capital intensive is more preferable than labor intensive?

It totally depends on what business you are running, such as a builder would want a labor intensive business, whilst a car maker would want a capital intensive business, disserent businesses need different things.

Electron hole

Electron hole

A gap left in the covalent bond when a valence electron gains sufficient energy to jump to the conduction band.

An electron hole is the conceptual and mathematical opposite of an electron, useful in the study of physics, chemistry, and electrical engineering. The concept describes the lack of an electron at a position where one could exist in an atom or atomic lattice. It is different from the positron, which is the antimatter analogue of the electron. Atoms with electron holes are defined as cations.

The electron hole was introduced into calculations for the following two situations:

If an electron is excited into a higher state it leaves a hole in its old state. This meaning is used in Auger electron spectroscopy (and other x-ray techniques), in computational chemistry, and to explain the low electron-electron scattering-rate in crystals (metals, semiconductors).
In crystals, band structure calculations lead to an effective mass for the charge carriers, which can be negative. Inspired by the Hall effect, Newton's law is used to attach the negative sign onto the charge.

Insulator

Insulator

A nonconducting material that provides electric isolation of two parts at different voltages. To accomplish this, an insulator must meet two primary requirements: it must have an electrical resistivity and a dielectric strength sufficiently high for the given application. The secondary requirements relate to thermal and mechanical properties. Occasionally, tertiary requirements relating to dielectric loss and dielectric constant must also be observed. A complementary requirement is that the required properties not deteriorate in a given environment and desired lifetime. See also Conductor (electricity).

Electric insulation is generally a vital factor in both the technical and economic feasibility of complex power and electronic systems. The generation and transmission of electric power depend critically upon the performance of electric insulation, and now plays an even more crucial role because of the energy shortage.

Semiconductor

Semiconductor

Any of various solid crystalline substances, such as germanium or silicon, having electrical conductivity greater than insulators but less than good conductors, and used especially as a base material for computer chips and other electronic devices.
An integrated circuit or other electronic component containing a semiconductor as a base material.

light emitting diode

Q What is a light emitting diode?

A light-emitting Diode (LED) is a semiconductor device that converts electrical energy into light energy. When put into a circuit, the current only travels in one direction. The most commonly used LED emits red light.

Clamper circuits

The circuits in Figure below are known as clampers or DC restorers. The corresponding netlist is in Figure below. These circuits clamp a peak of a waveform to a specific DC level compared with a capacitively coupled signal which swings about its average DC level (usually 0V). If the diode is removed from the clamper, it defaults to a simple coupling capacitor– no clamping.

What is the clamp voltage? And, which peak gets clamped? In Figure below (a) the clamp voltage is 0 V ignoring diode drop, (more exactly 0.7 V with Si diode drop). In Figure below, the positive peak of V(1) is clamped to the 0 V (0.7 V) clamp level. Why is this? On the first positive half cycle, the diode conducts charging the capacitor left end to +5 V (4.3 V). This is -5 V (-4.3 V) on the right end at V(1,4). Note the polarity marked on the capacitor in Figure below (a). The right end of the capacitor is -5 V DC (-4.3 V) with respect to ground. It also has an AC 5 V peak sinewave coupled across it from source V(4) to node 1. The sum of the two is a 5 V peak sine riding on a - 5 V DC (-4.3 V) level. The diode only conducts on successive positive excursions of source V(4) if the peak V(4) exceeds the charge on the capacitor. This only happens if the charge on the capacitor drained off due to a load, not shown. The charge on the capacitor is equal to the positive peak of V(4) (less 0.7 diode drop). The AC riding on the negative end, right end, is shifted down. The positive peak of the waveform is clamped to 0 V (0.7 V) because the diode conducts on the positive peak.
V(4) source voltage 5 V peak used in all clampers. V(1) clamper output from Figure above (a). V(1,4) DC voltage on capacitor in Figure (a). V(2) clamper output from Figure (b). V(3) clamper output from Figure (c).

Suppose the polarity of the diode is reversed as in Figure above (b)? The diode conducts on the negative peak of source V(4). The negative peak is clamped to 0 V (-0.7 V). See V(2) in Figure above.

The most general realization of the clamper is shown in Figure above (c) with the diode connected to a DC reference. The capacitor still charges during the negative peak of the source. Note that the polarities of the AC source and the DC reference are series aiding. Thus, the capacitor charges to the sum to the two, 10 V DC (9.3 V). Coupling the 5 V peak sinewave across the capacitor yields Figure above V(3), the sum of the charge on the capacitor and the sinewave. The negative peak appears to be clamped to 5 V DC (4.3V), the value of the DC clamp reference (less diode drop).

Describe the waveform if the DC clamp reference is changed from 5 V to 10 V. The clamped waveform will shift up. The negative peak will be clamped to 10 V (9.3). Suppose that the amplitude of the sine wave source is increased from 5 V to 7 V? The negative peak clamp level will remain unchanged. Though, the amplitude of the sinewave output will increase.

An application of the clamper circuit is as a “DC restorer” in “composite video” circuitry in both television transmitters and receivers. An NTSC (US video standard) video signal “white level” corresponds to minimum (12.5%) transmitted power. The video “black level” corresponds to a high level (75% of transmitter power. There is a “blacker than black level” corresponding to 100% transmitted power assigned to synchronization signals. The NTSC signal contains both video and synchronization pulses. The problem with the composite video is that its average DC level varies with the scene, dark vs light. The video itself is supposed to vary. However, the sync must always peak at 100%. To prevent the sync signals from drifting with changing scenes, a “DC restorer” clamps the top of the sync pulses to a voltage corresponding to 100% transmitter modulation. [ATCO]

REVIEW:
A capacitively coupled signal alternates about its average DC level (0 V).
The signal out of a clamper appears the have one peak clamped to a DC voltage. Example: The negative peak is clamped to 0 VDC, the waveform appears to be shifted upward. The polarity of the diode determines which peak is clamped.
An application of a clamper, or DC restorer, is in clamping the sync pulses of composite video to a voltage corresponding to 100% of transmitter power.


V(4) source voltage 5 V peak used in all clampers. V(1) clamper output from Figure above (a). V(1,4) DC voltage on capacitor in Figure (a). V(2) clamper output from Figure (b). V(3) clamper output from Figure (c).

Suppose the polarity of the diode is reversed as in Figure above (b)? The diode conducts on the negative peak of source V(4). The negative peak is clamped to 0 V (-0.7 V). See V(2) in Figure above.

The most general realization of the clamper is shown in Figure above (c) with the diode connected to a DC reference. The capacitor still charges during the negative peak of the source. Note that the polarities of the AC source and the DC reference are series aiding. Thus, the capacitor charges to the sum to the two, 10 V DC (9.3 V). Coupling the 5 V peak sinewave across the capacitor yields Figure above V(3), the sum of the charge on the capacitor and the sinewave. The negative peak appears to be clamped to 5 V DC (4.3V), the value of the DC clamp reference (less diode drop).

Describe the waveform if the DC clamp reference is changed from 5 V to 10 V. The clamped waveform will shift up. The negative peak will be clamped to 10 V (9.3). Suppose that the amplitude of the sine wave source is increased from 5 V to 7 V? The negative peak clamp level will remain unchanged. Though, the amplitude of the sinewave output will increase.

An application of the clamper circuit is as a “DC restorer” in “composite video” circuitry in both television transmitters and receivers. An NTSC (US video standard) video signal “white level” corresponds to minimum (12.5%) transmitted power. The video “black level” corresponds to a high level (75% of transmitter power. There is a “blacker than black level” corresponding to 100% transmitted power assigned to synchronization signals. The NTSC signal contains both video and synchronization pulses. The problem with the composite video is that its average DC level varies with the scene, dark vs light. The video itself is supposed to vary. However, the sync must always peak at 100%. To prevent the sync signals from drifting with changing scenes, a “DC restorer” clamps the top of the sync pulses to a voltage corresponding to 100% transmitter modulation. [ATCO]

REVIEW:
A capacitively coupled signal alternates about its average DC level (0 V).
The signal out of a clamper appears the have one peak clamped to a DC voltage. Example: The negative peak is clamped to 0 VDC, the waveform appears to be shifted upward. The polarity of the diode determines which peak is clamped.
An application of a clamper, or DC restorer, is in clamping the sync pulses of composite video to a voltage corresponding to 100% of transmitter power.

Defination of Ohm's Law

Ohm's Law defines the relationships between (P) power, (E) voltage, (I) current, and (R) resistance. One ohm is the resistance value through which one volt will maintain a current of one ampere.

( I ) Current is what flows on a wire or conductor like water flowing down a river. Current flows from negative to positive on the surface of a conductor. Current is measured in (A) amperes or amps.

( E ) Voltage is the difference in electrical potential between two points in a circuit. It's the push or pressure behind current flow through a circuit, and is measured in (V) volts.

( R ) Resistance determines how much current will flow through a component. Resistors are used to control voltage and current levels. A very high resistance allows a small amount of current to flow. A very low resistance allows a large amount of current to flow. Resistance is measured in ohms.

( P ) Power is the amount of current times the voltage level at a given point measured in wattage or watts.

Ohm's Law:

Uses of Ziner Diode

Zener diodes are widely used as voltage references and as shunt regulators to regulate the voltage across small circuits. When connected in parallel with a variable voltage source so that it is reverse biased, a Zener diode conducts when the voltage reaches the diode's reverse breakdown voltage. From that point on, the relatively low impedance of the diode keeps the voltage across the diode at that value.

In this circuit, a typical voltage reference or regulator, an input voltage, UIN, is regulated down to a stable output voltage UOUT. The intrinsic voltage drop of diode D is stable over a wide current range and holds UOUT relatively constant even though the input voltage may fluctuate over a fairly wide range. Because of the low impedance of the diode when operated like this, Resistor R is used to limit current through the circuit.
In the case of this simple reference, the current flowing in the diode is determined using Ohms law and the known voltage drop across the resistor R. IDiode = (UIN - UOUT) / RΩ
The value of R must satisfy two conditions:
R must be small enough that the current through D keeps D in reverse breakdown. The value of this current is given in the data sheet for D. For example, the common BZX79C5V6[1] device, a 5.6 V 0.5 W Zener diode, has a recommended reverse current of 5 mA. If insufficient current exists through D, then UOUT will be unregulated, and less than the nominal breakdown voltage (this differs to voltage regulator tubes where the output voltage will be higher than nominal and could rise as high as UIN). When calculating R, allowance must be made for any current through the external load, not shown in this diagram, connected across UOUT.
R must be large enough that the current through D does not destroy the device. If the current through D is ID, its breakdown voltage VB and its maximum power dissipation PMAX, then IDVB <>shunt, in this context, meaning connected in parallel, and voltage regulator being a class of circuit that produces a stable voltage across any load). In a sense, a portion of the current through the resistor is shunted through the Zener diode, and the rest is through the load. Thus the voltage that the load sees is controlled by causing some fraction of the current from the power source to bypass it—hence the name, by analogy with locomotive switching points.
Shunt regulators are simple, but the requirements that the ballast resistor be small enough to avoid excessive voltage drop during worst-case operation (low input voltage concurrent with high load current) tends to leave a lot of current flowing in the diode much of the time, making for a fairly wasteful regulator with high quiescent power dissipation, only suitable for smaller loads.
Zener diodes in this configuration are often used as stable references for more advanced voltage regulator circuits.
These devices are also encountered, typically in series with a base-emitter junction, in transistor stages where selective choice of a device centered around the avalanche/Zener point can be used to introduce compensating temperature co-efficient balancing of the transistor PN junction. An example of this kind of use would be a DC error amplifier used in a stabilized power supply circuit feedback loop system.

Nodal Analysis Electronic Circuit Theory

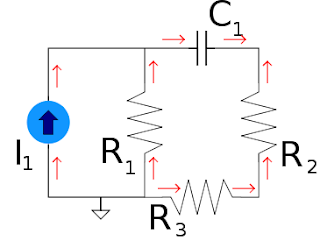
NODAL ANALYSIS

After simulating circuits for some time, I began to ask myself - how does this SPICE program work? What mathematical tricks does the code execute to simulate complex electrical circuits described by non-linear differential equations? After some searching and digging, some answers were uncovered. At the core of the SPICE engine is a basic technique called Nodal Analysis. It calculates the voltage at any node given all resistances (conductances) and current sources of the circuit. Whether the program is performing DC, AC, or Transient Analysis, SPICE ultimately casts its components (linear, non-linear and energy-storage elements) into a form where the innermost calculation is Nodal Analysis.

WHAT IS NODAL ANALYSIS?
Kirchoff discovered this: the total current entering a node equals the total current leaving a node! And, these currents can be described by an equation of voltages and conductances. If you have more than one node, then you get more than one equation describing the same system (simultaneous equations). The trick now is finding the voltage at each node that satisfies all of the equations simultaneously.
Circuit Example Here’s a simple circuit example.
Another way of stating the KC Law is this: the sum of currents in and out of a node is zero. This makes writing nodal equations a piece of cake. The two equations for the two circuit nodes look like this.
Because our mission is to calculate the node voltages, let’s reorganize the equations in terms of V1 and V2.
So here sit V1 and V2 in the middle of two different equations. The trick is finding the values of V1 and V2 that satisfy both equations. But how?

SOLUTION #1 – WORK THE EQUATIONS
Just roll up your sleeves and solve for V1 and V2. Before we begin we’ll make bookkeeping easy by writing the resistors in terms of total conductance: G11 = 1/R1 + 1/R2, G12 = -1/R2, G21 = -1/R2 and G22 = 1/R2+1/R3. The system equations now look like this.
First, solve the second equation for V1
Then, stick this into the first equation and solve for V2
Okay, it’s a little messy, but we’ve got V2 described by circuit conductances and Is only! After V2 is calculated numerically, stick it back into V1 = – G22 ∙V2 / G21 and there you have it, circuit voltages V1 and V2 that satisfy both system equations.

SOLUTION #2 – THE MATRIX
Solution #1 looks reasonable for simple circuits, but what about medium or large circuits? The bookkeeping of terms spins out of control quickly. What’s needed is a more methodical and efficient solution: Enter the Matrix. Here’s the set of nodal equations written in matrix form.
Or, in terms of total conductances and source currents
Treating each matrix as a variable, you can write
G ∙ v = i
In the matrix world, you can solve for a variable (almost) like any other algebraic equation. Solving for v you get
v = G-1∙ i
Where G-1 is the matrix inverse of G. ( 1 / G does not exist in the matrix world.) This equation is the central mechanism of the SPICE algorithm. Regardless of the analysis – AC, DC, or Transient – all components or their effects are cast into the conductance matrix G and the node voltages are calculated by v = G-1∙ i , or some equivalent method.

LINEAR DC ANALYSIS
Armed with Nodal Analysis and an Excel spreadsheet, you can perform Linear DC Analysis on the circuit above. Download and open the spreadsheet LINEAR_DC_ANALYSIS.XLS. Enter the circuit values under the variables shaded light blue.
R1
R2
R3
Is
10
1000
1000
1
How much voltage would you estimate at nodes 1 and 2? You can expect V1 = Is ∙ R1 =1 A ∙ 10 ohms = 10V. That’s because R2 and R3 have little effect on 10 ohms. At node 2, the simple R2-R3 divider should produce about V2 = 5V.
First, the spread sheet calculates the conductance matrix G
0.101
-0.001
-0.001
0.002
according to the equations
1/R1 + 1/R2
-1/R2
-1/R2
1/R2 + 1/R3
Next, Excel inverts G and multiplies the result G-1 by i to get v. ( See how Excels inverts and multiplies matrices below.)
G-1 x i = v
9.95
4.98
x
1
=
9.9502
4.98
502.49

0

4.9751
And there you have it, just like the SPICE engine, we’ve computed the circuit’s voltages! Pick other values for R1 like 1 or 100 Ω. Does the output scale up and down as expected? Change R2 or R3. Vary Is or change its polarity.
HANDS-ON DESIGN Try adding another resistor to the circuit. For example, place R4 in parallel with R3. Write out the nodal equations. Then include R3 in the cell formulas that form G. The Excel formulas should effectively calculate the following.
1/R1 + 1/R2
-1/R2
-1/R2
1/R2 + 1/R3 + 1/R4

THE SPICE CIRCUIT
To verify the results our nodal analysis, you can run a simulation of DC_LINEAR_CKT.CIR. or copy this netlist into a text file with the *.cir extension.LINEAR_DC_CKT.CIR - SIMPLE CIRCUIT FOR NODAL ANALYSIS
*
IS 0 1 DC 1A
*
R1 1 0 10
R2 1 2 1K
R3 2 0 1K
*
* ANALYSIS
.TRAN 1MS 10MS
* VIEW RESULTS
.PRINT TRAN V(1) V(2)
.PROBE
.END
Although it runs a Transient Analysis, it essentially computes a DC Linear Analysis because no non-linear elements or charge-storage devices exist in the circuit. Plot V(1) and V(2). Utilize the cursor, if needed, to get an accurate measurement. Do the voltages from SPICE and Excel agree?

EXCEL MATRIX OPERATIONS
Excel provides handy matrix functions for getting our hands on the nodal analysis example. Matrix functions are entered like any other Excel function except for one trick. Instead of pressing ENTER after entering a function, you need to hit CTRL-SHIFT-ENTER simultaneously!
► MATRIX INVERSION
Here are the steps to calculate the matrix inverse of G in the file LINEAR_DC_ANALYSIS.xls.
1. Select the range of cells (B16:C17) to hold the inverse result.2. Type the formula MINVERSE(B10:C11) where B10:C11 defines the matrix to be inverted.3. Press CTRL-SHIFT-ENTER.
► MATRIX MULTIPLICATION
Multiplying two matrices is just as easy.
1. Select the cells (G16:G17) to hold the multiplication result.2. Type the formula MMULT(B16:C17, E16:E17) where B16:C17 represents the square matrix and E16:E17 represents column matrix to be multiplied.3. Press CTRL-SHIFT-ENTER.

THE MATRIX SOLUTION - GOOD NEWS, BAD NEWS
The good news is that the matrix form of system equations can be easily expanded to larger circuits. The bad news lies in finding v. There are several paths to answer. Why so many? Some are more efficient then others. Briefly, here are three techniques to solve the matrix equation for v.
1. MATRIX INVERSION
Although a very straight forward formula exists (Cramer’s Rule) to calculate the inverse of G, it’s very inefficient for large matrices.
2. GAUSSIAN ELIMINATION
Matrix equations posses an amazing character trait! You can scale, add, or subtract rows of G and i without disturbing the solution to v. By cleverly choosing these operations, you can transform G into an Upper Triangular matrix, where all of the elements below the diagonal are zero! This makes finding v a snap using a technique called Backward Substitution. This method requires much less computational effort than Matrix Inversion.
3. LU FACTORIZATION
For maximum efficiency, SPICE actually uses an extension of Gaussian Elimination. The conductance matrix G is first factored into two matrices G = L U where L (Lower Triangular) stores the scale factors of Gaussian Elimination and U (Upper Triangular) stores the result of Gaussian Elimination. Then, the equation is solved for the node voltages
v = U-1 L-1 i
The inverses of L and U may not actually calculated. Instead, the equivalent is achieved by Forward and Backward Substitution steps. The advantage over Gaussian Elimination is that v can be solved repeatedly for different current sources i by only performing the forward and backward substitution steps. This comes in handy when SPICE performs different analysis like sensitivity, noise and distortion for the same circuit!

WHAT ABOUT VOLTAGE SOURCES?
You may have noticed that nodal analysis does not accommodate a voltage source. What can be done? In the early days, voltage sources were defined with a small series resistor, representing the internal resistance of the source. Then, the V with series R was converted into its Norton Equivalent of I with parallel R. This alternate current source fit nicely into the Nodal System and all was right with the world.
Later, a clever method was hatched to include voltage-defined components called Modified Nodal Analysis (MNA). In this system, much of the equations looked just like Nodal Analysis with rows of equations added describing the influence of the voltage sources.

Mesh analysis Electronic Circuit Theory

Mesh analysis Electronic Circuit Theory


In the previous tutorial we saw that complex circuits such as bridge or T-networks can be solved using "Kirchoff's Circuit Laws". While Kirchoff´s Laws give us the basic method for analysing any complex electrical circuit, there are ways of improving upon this method by using Mesh Current Analysis or Nodal Voltage Analysis that results in a lessening of the math's involved and when large networks are involved this reduction in maths can be a big advantage.

For example, consider the circuit from the previous section.
Mesh Analysis Circuit
One simple method of reducing the amount of math's involved is to do Kirchoff´s First Current Law equations to determine the currents, I1 and I2 flowing in the two resistors and there is no need to calculate the current I3 as its just the sum of I1 and I2. Then the Second Voltage Law simply becomes:
Equation No 1 : 10 = 50I1 + 40I2
Equation No 2 : 20 = 40I1 + 60I2
therefore, one line of math's calculation have been saved.
Mesh Current Analysis
A more easier method of solving the above circuit is by using Mesh Current Analysis or Loop Analysis which is also sometimes called "Maxwell´s Circulating Currents" method. Instead of labelling the branch currents we need to label each "closed loop" with a circulating current. As a general rule of thumb, only label inside loops in a clockwise direction with circulating currents as the aim is to cover all the elements of the circuit at least once. Any required branch current may be found from the appropriate loop or mesh currents as before using Kirchoff´s method.
For example: : i1 = I1 , i2 = -I2 and I3 = I1 - I2
We now write Kirchoff´s second voltage law equations in the same way as before to solve them but the advantage of this method is that it ensures that the information obtained from the circuit equations is the minimum required to solve the circuit as the information is more general and can easily be put into a matrix form.
For example, consider the circuit from the previous section.

These equations can be solved quite quickly by using a single mesh impedance matrix Z. Each element ON the principal diagonal will be "positive" and is the total impedance of each mesh. Where as, each element OFF the principal diagonal will either be "zero" or "negative" and represents the circuit element connecting all the appropriate meshes. This then gives us a matrix of:

Where:
[ V ] gives the total battery voltage for loop 1 and then loop 2.
[ I ] states the names of the loop currents which we are trying to find.
[ R ] is called the resistance matrix.
and this gives I1 as -0.143 Amps and I2 as -0.429 Amps
As : I3 = I1 - I2
The current I3 is therefore given as : -0.143 - (-0.429) = 0.286 Amps
which is the same value of 0.286 amps, we found using Kirchoff´s circuit law in the previous tutorial.
Page Summary.
This "look-see" method of circuit analysis is probably the best of all the circuit analysis methods with the basic procedure for solving Mesh Current Anaysis equations is as follows:
1. Label all the internal loops with circulating currents. (I1, I2, ...IL etc)

2. Write the [ L x 1 ] column matrix [ V ] giving the sum of all voltage sources in each loop.

3. Write the [ L x L ] matrix, [ R ] for all the resistances in the circuit as follows;
R11 = the total resistance in the first loop.
Rnn = the total resistance in the Nth loop.
RJK = the resistance which directly joins loop J to Loop K.
4. Write the matrix or vector equation [V] = [R] x [I] where [I] is the list of currents to be found.

Capacitors

Capacitor

A capacitor or condenser is a passive electronic component consisting of a pair of conductors separated by a dielectric. When a voltage potential difference exists between the conductors, an electric field is present in the dielectric. This field stores energy and produces a mechanical force between the plates. The effect is greatest between wide, flat, parallel, narrowly separated conductors.
An ideal capacitor is characterized by a single constant value, capacitance, which is measured in farads. This is the ratio of the electric charge on each conductor to the potential difference between them. In practice, the dielectric between the plates passes a small amount of leakage current. The conductors and leads introduce an equivalent series resistance and the dielectric has an electric field strength limit resulting in a breakdown voltage.
Capacitors are widely used in electronic circuits to block the flow of direct current while allowing alternating current to pass, to filter out interference, to smooth the output of power supplies, and for many other purposes. They are used in resonant circuits in radio frequency equipment to select particular frequencies from a signal with many frequencies.

Integrated Circuits

Integrated circuit

In electronics, an integrated circuit (also known as IC, microcircuit, microchip, silicon chip, or chip) is a miniaturized electronic circuit (consisting mainly of semiconductor devices, as well as passive components) that has been manufactured in the surface of a thin substrate of semiconductor material. Integrated circuits are used in almost all electronic equipment in use today and have revolutionized the world of electronics.
A hybrid integrated circuit is a miniaturized electronic circuit constructed of individual semiconductor devices, as well as passive components, bonded to a substrate or circuit board.

Clipper Circuit

A circuit which removes the peak of a waveform is known as a clipper. A negative clipper is shown in Figure below. This schematic diagram was produced with Xcircuit schematic capture program. Xcircuit produced the SPICE net list Figure below, except for the second, and next to last pair of lines which were inserted with a text editor.

During the positive half cycle of the 5 V peak input, the diode is reversed biased. The diode does not conduct. It is as if the diode were not there. The positive half cycle is unchanged at the output V(2) in Figure below. Since the output positive peaks actually overlays the input sinewave V(1), the input has been shifted upward in the plot for clarity. In Nutmeg, the SPICE display module, the command “plot v(1)+1)” accomplishes this. During the negative half cycle of sinewave input of Figure above, the diode is forward biased, that is, conducting. The negative half cycle of the sinewave is shorted out. The negative half cycle of V(2) would be clipped at 0 V for an ideal diode. The waveform is clipped at -0.7 V due to the forward voltage drop of the silicon diode. The spice model defaults to 0.7 V unless parameters in the model statement specify otherwise. Germanium or Schottky diodes clip at lower voltages.
Closer examination of the negative clipped peak (Figure above) reveals that it follows the input for a slight period of time while the sinewave is moving toward -0.7 V. The clipping action is only effective after the input sinewave exceeds -0.7 V. The diode is not conducting for the complete half cycle, though, during most of it.

Diode D1 clips the negative peak at -0.7 V as before. The additional diode D2 conducts for positive half cycles of the sine wave as it exceeds 0.7 V, the forward diode drop. The remainder of the voltage drops across the series resistor. Thus, both peaks of the input sinewave are clipped

The most general form of the diode clipper is shown in Figure below. For an ideal diode, the clipping occurs at the level of the clipping voltage, V1 and V2. However, the voltage sources have been adjusted to account for the 0.7 V forward drop of the real silicon diodes. D1 clips at 1.3V +0.7V=2.0V when the diode begins to conduct. D2 clips at -2.3V -0.7V=-3.0V when D2 conducts

The clipper in Figure above does not have to clip both levels. To clip at one level with one diode and one voltage source, remove the other diode and source.

There is also a zener diode clipper circuit in the “Zener diode” section. A zener diode replaces both the diode and the DC voltage source.
A practical application of a clipper is to prevent an amplified speech signal from overdriving a radio transmitter in Figure below. Over driving the transmitter generates spurious radio signals which causes interference with other stations. The clipper is a protective measure

A sinewave may be squared up by overdriving a clipper. Another clipper application is the protection of exposed inputs of integrated circuits. The input of the IC is connected to a pair of diodes as at node “2” of Figure above . The voltage sources are replaced by the power supply rails of the IC. For example, CMOS IC's use 0V and +5 V. Analog amplifiers might use ±12V for the V1 and V2 sources.
REVIEW
A resistor and diode driven by an AC voltage source clips the signal observed across the diode.
A pair of anti-parallel Si diodes clip symmetrically at ±0.7V
The grounded end of a clipper diode(s) can be disconnected and wired to a DC voltage to clip at an arbitrary level.
A clipper can serve as a protective measure, preventing a signal from exceeding the clip limits

The Zener diode

Zener diode

A Zener diode is a type of diode that permits current in the forward direction like a normal diode, but also in the reverse direction if the voltage is larger than the breakdown voltage known as "Zener knee voltage" or "Zener voltage". The device was named after Clarence Zener, who discovered this electrical property.
A conventional solid-state diode will not allow significant current if it is reverse-biased below its reverse breakdown voltage. When the reverse bias breakdown voltage is exceeded, a conventional diode is subject to high current due to avalanche breakdown. Unless this current is limited by external circuitry, the diode will be permanently damaged. In case of large forward bias (current in the direction of the arrow), the diode exhibits a voltage drop due to its junction built-in voltage and internal resistance. The amount of the voltage drop depends on the semiconductor material and the doping concentrations.
A Zener diode exhibits almost the same properties, except the device is specially designed so as to have a greatly reduced breakdown voltage, the so-called Zener voltage. A Zener diode contains a heavily doped p-n junction allowing electrons to tunnel from the valence band of the p-type material to the conduction band of the n-type material. In the atomic scale, this tunneling corresponds to the transport of valence band electrons into the empty conduction band states; as a result of the reduced barrier between these bands and high electric fields that are induced due to the relatively high levels of dopings on both sides. A reverse-biased Zener diode will exhibit a controlled breakdown and allow the current to keep the voltage across the Zener diode at the Zener voltage. For example, a diode with a Zener breakdown voltage of 3.2 V will exhibit a voltage drop of 3.2 V if reverse bias voltage applied across it is more than its Zener voltage. However, the current is not unlimited, so the Zener diode is typically used to generate a reference voltage for an amplifier stage, or as a voltage stabilizer for low-current applications.
The breakdown voltage can be controlled quite accurately in the doping process. While tolerances within 0.05% are available, the most widely used tolerances are 5% and 10%.
Another mechanism that produces a similar effect is the avalanche effect as in the avalanche diode. The two types of diode are in fact constructed the same way and both effects are present in diodes of this type. In silicon diodes up to about 5.6 volts, the Zener effect is the predominant effect and shows a marked negative temperature coefficient. Above 5.6 volts, the avalanche effect becomes predominant and exhibits a positive temperature coefficient.

In a 5.6 V diode, the two effects occur together and their temperature coefficients neatly cancel each other out, thus the 5.6 V diode is the component of choice in temperature-critical applications.
Modern manufacturing techniques have produced devices with voltages lower than 5.6 V with negligible temperature coefficients, but as higher voltage devices are encountered, the temperature coefficient rises dramatically. A 75 V diode has 10 times the coefficient of a 12 V diode.
All such diodes, regardless of breakdown voltage, are usually marketed under the umbrella term of "Zener diode".

Electric Circuit

Electric circuit, unbroken path along which an electric current exists or is intended or able to flow. A simple circuit might consist of an electric cell (the power source), two conducting wires (one end of each being attached to each terminal of the cell), and a small lamp (the load) to which the free ends of the wires leading from the cell are attached. When the connections are made properly, current flows, the circuit is said to be "closed," and the lamp will light. The current flows from the cell along one wire to the lamp, through the lamp, and along the other wire back to the cell. When the wires are disconnected, the circuit is said to be "open" or "broken." In practice, circuits are opened by such devices as switches, fuses, and circuit breakers (see fuse, electric; circuit breaker; short circuit). Two general circuit classifications are series and parallel. The elements of a series circuit are connected end to end; the same current flows through its parts one after another. The elements of a parallel circuit are connected so that each component has the same voltage across its terminals; the current flow is divided among its parts. When two circuit elements are connected in series, their effective resistance (impedance if the circuit is being fed alternating current) is equal to the sum of the separate resistances; the current is the same in each component throughout the circuit. When circuit elements are connected in parallel, the total resistance is less than that of the element having the least resistance, and the total current is equal to the sum of the currents in the individual branches. A battery-powered circuit is an example of a direct-current circuit; the voltages and currents are constant in magnitude and do not vary with time. In alternating-current circuits, the voltage and current periodically reverse direction with time. A standard electrical outlet supplies alternating current. Lighting circuits and electrical machinery use alternating current circuits. Many other devices, including computers, stereo systems, and television sets, must first convert the alternating current to direct current. That is done by a special internal circuit usually called a power supply. A digital circuit is a special kind of electronic circuit used in computers and many other devices. Magnetic circuits are analogous to electric circuits, where magnetic materials are regarded as conductors of magnetic flux. Magnetic circuits can be part of an electric circuit; a transformer is an example. Equivalent circuits are used in circuit analysis as a modeling tool; a simple circuit made up of a resistor, and an inductor might be used to electrically represent a loudspeaker. Electrical circuits can also be used in other fields of studies. In the study of heat flow, for example, a resistor is used to represent thermal insulation. Operating electric circuits can be used for general problem solving (as in an analog computer).